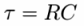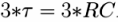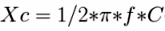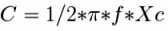Как просто определить емкость конденсатора подручными средствами

Иногда, когда на конденсаторе отсутствует маркировка или нет доверия к указанным на его корпусе параметрам, требуется как-то узнать реальную емкость. Но как это сделать, не имея специального оборудования?

Безусловно, если под рукой есть мультиметр с возможностью измерения емкости или C-метр с подходящим диапазоном измерения емкостей, то проблема перестает быть таковой. Но что же делать, если в наличии только простой бытовой мультиметр и какой-нибудь блок питания, а измерить емкость конденсатора необходимо здесь и сейчас? На помощь в этом случае придут известные законы физики, которые позволят с достаточной степенью точности измерить емкость.

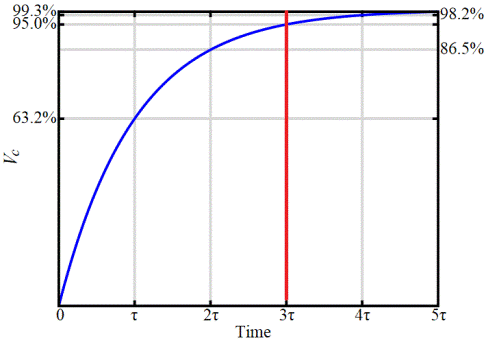
Рассмотрим сначала простой способ измерения емкости электролитического конденсатора подручными средствами. Как известно, при заряде конденсатора от источника постоянного напряжения через резистор, имеет место закономерность, по которой напряжение на конденсаторе станет экспоненциально приближаться к напряжению источника, и в пределе когда-нибудь, наконец, его достигнет.

Но чтобы долго не ждать, можно задачу себе упростить. Известно, что за время, равное 3*RC, напряжение на конденсаторе в процессе зарядки достигнет 95% напряжения, приложенного к RC-цепочке. Значит, зная напряжение блока питания, номинал резистора, и вооружившись секундомером, можно легко измерить постоянную времени, а точнее — троекратную постоянную времени для большей точности, и вычислить затем емкость конденсатора по известной формуле.

Для примера рассмотрим далее эксперимент. Допустим, есть у нас электролитический конденсатор, на котором присутствует какая-то маркировка, но мы ей не особо доверяем, так как конденсатор давно валялся в закромах, и мало ли высох, в общем нужно измерить его емкость. Например, на конденсаторе написано 6800мкф 50в, но нужно узнать точно.

Шаг №1. Берем резистор номиналом 10кОм, измеряем его сопротивление мультиметром, поскольку своему мультиметру в этом эксперименте мы будем изначально доверять. Например, получилось сопротивление 9840 Ом.

Шаг №2. Включаем блок питания. Поскольку мультиметру мы доверяем больше, чем калибровке шкалы (если таковая имеется) блока питания, переводим мультиметр в режим измерения постоянного напряжения, и подключаем его к выводам блока питания. Выставляем напряжение блока питания на 12 вольт, чтобы мультиметр точно показал 12,00 В. Если напряжение блока питания не регулируется, то просто замеряем его и записываем.

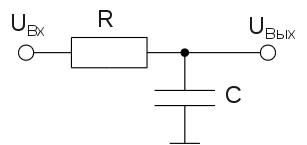
Шаг №3. Собираем RC-цепочку из резистора и конденсатора, емкость которого нужно измерить. Конденсатор закорачиваем на время так, чтобы его легко можно было раскоротить.

Шаг №4. Подключаем RC-цепочку к блоку питания. Конденсатор все еще закорочен. Измеряем мультиметром еще раз напряжение, подаваемое на RC-цепочку, и фиксируем это значение для верности на бумаге. К примеру, оно так и осталось 12,00 В, или таким же, каким было в начале.

Шаг №5. Вычисляем 95% от этого напряжения, например если 12 вольт, то 95% — это 11,4 вольта. Теперь мы знаем, что за время, равное 3*RC, конденсатор зарядится до 11,4 В.

Шаг №6. Берем в руки секундомер, и раскорачиваем конденсатор, начинаем одновременно отсчет времени. Фиксируем время, за которое напряжение на конденсаторе достигло 11,4 В, это и будет 3*RC.

Шаг №7. Производим вычисления. Получившееся время в секундах делим на сопротивление резистора в омах, и на 3. Получаем значение емкости конденсатора в фарадах.

Например: время получилось 220 секунд (3 минуты и 40 секунд). Делим 220 на 3 и на 9840, получаем емкость в фарадах. В нашем примере получилось 0,007452 Ф, то есть 7452 мкф, а на конденсаторе написано 6800 мкф. Таким образом, в допустимые 20% отклонение емкости уложилось, поскольку составило примерно 9,6%.

Но как быть с неполярными конденсаторами малых емкостей? Если конденсатор керамический или полипропиленовый, то здесь поможет переменный ток и знание о емкостном сопротивлении.

К примеру, есть конденсатор, емкость его предположительно несколько нанофарад, и известно, что в цепи переменного тока работать он может. Для выполнения измерений потребуется сетевой трансформатор со вторичной обмоткой, скажем, на 12 вольт, мультиметр, и все тот же резистор на 10 кОм.

Шаг №1. Собираем RC-цепь, и подключаем ее ко вторичной обмотке трансформатора. Затем включаем трансформатор в сеть.

Шаг №2. Измеряем мультиметром переменное напряжение на конденсаторе, затем — на резисторе.

Шаг №3. Производим вычисления. Сначала вычисляем ток через резистор, — делим напряжение на нем на значение его сопротивление. Поскольку цепь последовательная, то переменный ток через конденсатор точно такой же величины. Делим напряжение на конденсаторе на ток через резистор (ток через конденсатор такой же), получаем значение емкостного сопротивления Хс. Зная емкостное сопротивление и частоту тока (50 Гц), вычисляем емкость нашего конденсатора.

Например: на резисторе 7 вольт, а на конденсаторе 5 вольт. Мы посчитали, что ток через резистор в этом случае 700 мкА, следовательно и через конденсатор — такой же. Значит емкостное сопротивление конденсатора на частоте 50 Гц составляет 5/0,0007 = 7142,8 Ом. Емкостное сопротивление Xc = 1/6,28fC, следовательно C = 445 нф, то есть номинал 470 нф.

Описанные здесь способы являются весьма грубыми, поэтому применять их можно только тогда, когда других вариантов просто нет. В иных случаях лучше пользоваться специальными измерительными приборами.

Профессиональное развитие начинается здесь: Телеграмм канал Домашняя электрика

Источник

В помощь изучающему электронику

Формулы, вычисления, .

— Емкость, конденсатор —

Данный справочник собран из разных источников. Но на его создание подтолкнула небольшая книжка «Массовой радиобиблиотеки» изданная в 1964 году, как перевод книги О. Кронегера в ГДР в 1961 году. Не смотря на такую ее древность, она является моей настольной книгой (наряду с несколькими другими справочниками). Думаю время над такими книгами не властно, потому что основы физики, электро и радиотехники (электроники) незыблемы и вечны.

Единица емкости фарада (ф) — емкость такого конденсатора, увеличение заряда которого на 1 кулон (к) вызывает повышение разности потенциалов между обкладками конденсатора на 1 в:

C = Q/U [ф] где:

С — емкость, ф;
Q — количество электричества, к;
U — напряжение, в.
На практике обычно пользуются значительно более мелкими единицами емкости см Таблицу 1.

Напряженность поля Е между двумя пластинами (обкладками) конденсатора вычисляется по формуле

E = U/a [в\м] где:

U — напряжение между обкладками, S;
a — расстояние между пластинами, м.
Так как на обеих пластинах конденсатора накапливаются заряды противоположной полярности, то эти пластины взаимно притягиваются с силой F. Она рассчитывается в ньютонах (н) следующим образом:

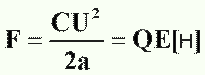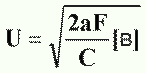Накопленная в конденсаторе энергия, определяемая в джоулях (дж) , равна:

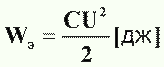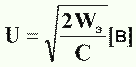С —емкость, ф;
U—напряжение, в.
Во время заряда или разряда конденсатора величина протекающего тока изменяется. Мгновенное значение тока выражается формулой: гдe:

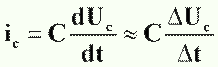
ΔU_с — изменение напряжения на обкладках конденсатора за время Δt.
Эта формула имеет важное практическое значение, она показывает, что напряжение на конденсаторе при его заряде не сразу достигает своего максимального значения.

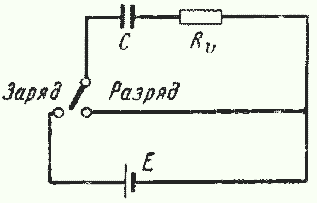
Точно так же при разряде конденсатора напряжение убывает до нуля не сразу, а постепенно. Конденсатору всегда присущи потери, которые можно представить себе в виде омического сопротивления, соединенного последовательно или параллельно с конденсатором. Если сопротивление Rv включено последовательно с конденсатором (без потерь) то при заряде его от источника, э.д.с. которого равна Е, а внутреннее сопротивление равно нулю (рис. 2), зарядный ток i_зар и напряжение на обкладках конденсатора U_с будут меняться по закону

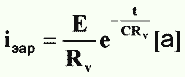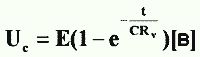Е — э. д. с., в;
t — время, прошедшее с момента начала заряда, сек.
Величина CR_V имеет размерность времени, так как (а • сек/ в) * (в/a) = сек, Ее называют постоянной времени τ конденсатора и она характеризует качество конденсатора и требует учета на временах приближающихся к собственной τ. Rv определяет и мощность потерь при работе конденсатора в цепях переменного тока.

По тем же законам изменяется ток и при включении последовательно с конденсатором резистора R.

Причем время нарастания для RC цепочки равно:

T_a = 2,2 R C = 2,2 τ

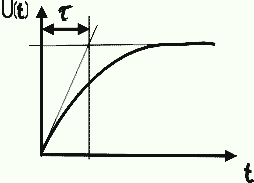
А время нарастания определяется по графику переходного процесса:

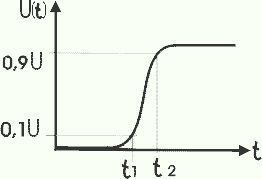
Здесь T_a = t₂ — t₁. Следует обратить ваше внимание, что Э.Д.С. самоиндукции в переключающих схемах с большими паразитными индуктивностями определяется максимальной скоростью нарастания тока. Контроль и точное измерение (или по крайней мере достаточно точная оценка) скорости нарастания тока является весьма важным для обеспечения надежности таких ключей.

При Δt -> 0, получаем мгновенные значения скорости изменения тока. Оно наиболее точно характеризует характер изменения величины и может быть записано в виде:

_{i=lim ΔI/Δt =dI/dt}
Δt->0

С — емкость, мкф;
R_v— сопротивление, Мом_.
При разрядке:

По прошествии интервала времени t_н ≈0,7 τ величина напряжения (или тока) достигает половины максимального значения.
Известно много схем, свойства которых обусловлены величиной постоянной времени.
Дифференцирующая цепь (рис. 3):

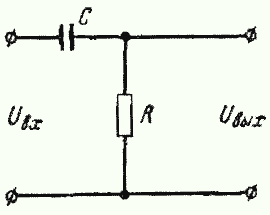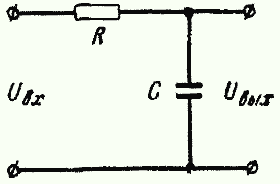На рис 3 и 4 показаны две различные цепи, рис. 3 — дифференцирующая, а на рис. 4 — интегрирующая. Но не смотря на разные свойства и назначения цепей, процессы зарядки емкости проходящие в них проходят одинаково и описываются одинаковыми формулами. Постоянная времени τ характеризует скорость заряда или разряда конденсатора:
τ = C Rv [сек]
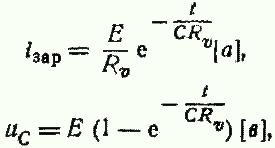τ = RC ≤ 0,159/f[сек]
где: f частота гц. Интегрирующая цепь (рис. 4)
τ = RC ≥ 0,159/f [сек]
При расчете конденсаторов приходится учитывать абсолютную диэлектрическую проницаемость среды е, которую можно представить в виде произведения двух величин:
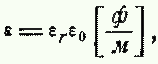где: εr— относительная диэлектрическая проницаемость (или просто диэлектрическая проницаемость) — величина, показывающая, во сколько раз сила взаимодействия между электрическими зарядами в данной среде меньше, чем в вакууме; ε0 = 8,86 • 10 -12 ф/м= 8,86 пф/м — электрическая постоянная, численно равная абсолютной диэлектрической проницаемости вакуума. Диэлектрическая проницаемость воздуха равна единице (ег= 1). Значения диэлектрической проницаемости некоторых материалов приведены в табл. 4.

Таблица 4

Материал	ε r	Пробивное напряжение кВ/мм	tg φ (вч/нч)
Бакелит	4 -4,6	10-40	0,05-0,12 / —
Бумага конденсаторная	3,5	20	0,01 / —
Винипласт	4,1	15
Вода	87,83
Воздух	1,000574
Гетинакс А,Б,В,Г	5-7	6,0 -817-30	0,07-0,1 / —
Дерево (береза)	3-4	40-60
Канифоль	3,5	10-15	0,01 / —
Лакоткань шелк	3,8-4,5	8-60	0,04-0,08 / —
Стекло	4 —10	20-30	0,0005-0,001 / 0,001
Стеклотекстолит	7,5 -8,0	10-12	0,01-0,1 / —
Слюда мусковит	6,8 —7,2	85-95	0,004-0,007 / 0,0002
Керамика	2 000—3 000
Тиконд (керамика)	70-150	10-12	0,0004 / 0,0004
Текстолит А/Вч	7,5-8,5	2-8	0,1-0,15 / 0,07
Масло конденсаторное	2,15	80-90	— /0,0001
Шелк натуральный	4-5	—
Фарфор эл-тех	6, 5	20	0,0004-0,0008 / —
Фторопласт 4	1,9-2,2	13-15	— / 0,0002-0,0003
Янтарь	2,7-2,9	20-30
TiO2	91	— / 0,004
BaTiO2	1500	— / 0,0159

Вч -на частоте 1 Мгц; Нч на частоте 50 гц. Емкость конденсатора, состоящего из двух плоских пластин , где

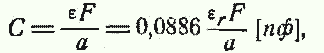
а — расстояние между пластинами (толщина диэлектрика), см.
Для конденсатора с числом пластин п емкость Для конденсатора с многослойным диэлектриком справедливо выражение ; Емкость коаксиального кабеля где:

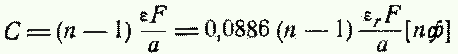
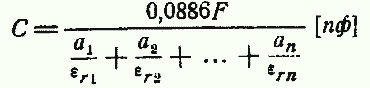
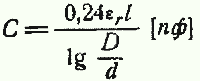
I —длина кабеля, см;
D — внутренний диаметр наружного проводника, см;
d — внешний диаметр внутреннего проводника, см.
Емкость двухпроводной линии где:

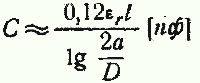
а —расстояние между проводами, см;
D — диаметр провода, см.
Емкость прямого провода, параллельного земле (при условии l>h>D),

Источник